Energia reticolare e costante di Madelung
Analizziamo il reticolo cubico a facce centrate del cloruro di sodio (![]() Na+,
Na+, ![]() Cl-). Se consideriamo il cubo costituito da 8 cubi più piccoli di identiche dimensioni (mi prendo la libertà di chiamarli cubetti), avremo 4 cubetti disposti sopra il piano centrale e altri quattro sotto di esso. Gli 8 cubetti presentano un vertice in comune in cui è centrato lo ione Na+.
Cl-). Se consideriamo il cubo costituito da 8 cubi più piccoli di identiche dimensioni (mi prendo la libertà di chiamarli cubetti), avremo 4 cubetti disposti sopra il piano centrale e altri quattro sotto di esso. Gli 8 cubetti presentano un vertice in comune in cui è centrato lo ione Na+.
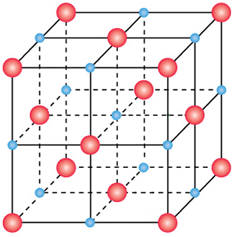

Lo ione Na+ centrale è a contatto diretto con 6 ioni cloro (![]() ) in coordinazione ottaedrica come è meglio evidenziato nella figura che segue. La distanza dal centro dello ione Na+ al centro degli ioni cloro corrisponde, dal punto di vista geometrico, al lato di cubetti che indicheremo con "r".
) in coordinazione ottaedrica come è meglio evidenziato nella figura che segue. La distanza dal centro dello ione Na+ al centro degli ioni cloro corrisponde, dal punto di vista geometrico, al lato di cubetti che indicheremo con "r".

L'energia potenziale che compete a questa parte del sistema, negativa perchè derivante da una forza attrattiva, considerando le sei cariche negative, vale:
 |
(1) |
Lo ione Na+ centrale interagisce, questa volta in termini repulsivi, con 12 altri ioni sodio (![]() ) disposti su tre piani e in maniera alternata (lati e vertici dei piani). Nella figura seguente viene evidenziata in verde la distanza di interazione tra lo ione centrale è uno ione sodio presente al vertice del piano centrale.
) disposti su tre piani e in maniera alternata (lati e vertici dei piani). Nella figura seguente viene evidenziata in verde la distanza di interazione tra lo ione centrale è uno ione sodio presente al vertice del piano centrale.
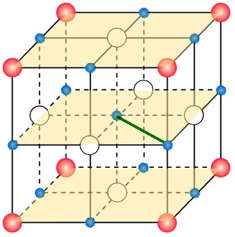
Tutte le distanze consistono nelle diagonali delle facce quadrate dei cubetti e pertanto equivalgono tutte al prodotto del lato per la radice quadrata di due. L'energia potenziale, ricavabile come fatto per la (1), risulta pertanto
| (2) |
Ai vertici del cubo grande (vertici dei piano superiore ed inferiore) sono presenti otto ioni cloro con i quali lo ione sodio interagisce in senso attrattivo.
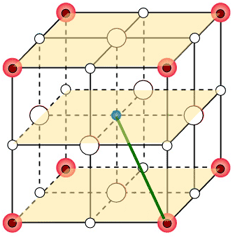
La distanza tra lo ione sodio e ciascuno degli ioni cloro, in questo caso, equivale alla diagonale (distanza vertice-vertice opposto) dei cubetti. Il suo valore pertanto risulta uguale al prodotto del lato dei cubetti per la radice quadrata di tre. L'energia potenziale che competa a questa interazione sarà:
| (3) |
Se si vuole ancora estendere il livello delle interazioni, si può passare agli ioni in posizione ottaedrica a distanza doppia rispetto a r:
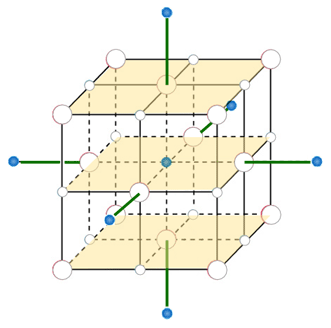
| (4) |
Si deve ancora andare avanti, ma noi ci fermiamo a questo livello. L'energia potenziale di tipo coulombiano complessiva è la somma dei termini ricavati finora e di altri di cui non ci occuperemo:
| (5) |
| (6) |
| evidenziando | (7) |
| Indicando con Md (Costante di Madelung) la serie numerica tra parentesi cambiata di segno |
| (8) |
| Per una mole di sostanza bisogna moltiplicare per il numero di Avogadro (NA) |
| (9) |
La formula ottenuta va letta nel modo seguente:
L'energia potenziale per una mole di coppie ioniche sistemate ordinatamente in un cristallo è uguale a quella posseduta da una mole di coppie ioniche moltiplicata per una costante caratteristica dell'assetto cristallino, detta costante di Madelung.
Le costanti di Madelung, lunghe e complicate da ottenere, sono state calcolate per vati tipi di assetti cristallini e assumono valori sempre maggiori di 1 (vedi sui libri e sulla tabella in questa paagina). Questo significa che l'energia che compete ad una mole di cristallo solido, in valore assoluto, è sempre maggiore a quella che compete ad una mole di coppie ioniche discrete e pertanto, considerando il segno, determina una notevole stabilizzazione dell'assetto cristallino rispetto alle coppie ioniche. Le Energie valutate sperimentalmente per la dissociazione di varie sostenze cristalline, sono in linea con quelle calcolate utilizzando la formula (9), e l'accordo diventa migliore se si considera anche la parte di energia dovuta alla repulsione delle nuvole elettroniche degli ioni.
NOTA: disposizione spaziale tridimensionale e interattiva per NaCl ( JSmol view )