Funzioni d'onda orbitale e probabilità radiale

Le soluzioni delle equazioni d'onda di Schrödinger per l'atomo di idrogeno sono fornite in coordinate polari sferiche. Le funzioni risultanti sono costituite dal prodotto di una parte radiale (distanza dal nucleo) che caratterizzerà l'estensione dell'orbitale e di una parte angolare (valore della funzione per effetto della rotazione Θ e Φ) che in definitiva determinerà quello che chiameremo "forma" dell'orbitale.

dove r è la distanza dal nucleo (0infinito), Θ è l'angolo che il raggio vettore produce con il verso positivo dell'asse verticale z (02π), Φ è l'angolo orizzontale tra il raggio vettore e il verso positivo dell'asse x nel piano xy.
Indicando con a₀ il raggio di BOHR (0.5291 Å), ecco alcune funzioni soluzioni dell'equazione di Schrödinger per l'atomo di idrogeno (ho usato il puntino grosso per separare la parte radiale da quella angolare):

orbitale 1s ψ(1,0,0) ψ1s
orbitale 2s ψ(2,0,0) ψ2s
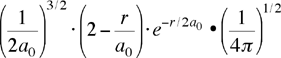orbitale 2pz ψ(2,1,0) ψ2pz
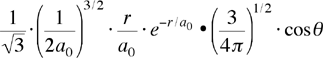orbitale 2px ψ(2,1,+1) ψ2px
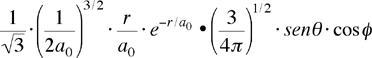orbitale 2py ψ(2,1,-1) ψ2py

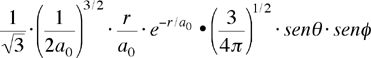Per gli orbitali di tipo s la parte angolare rimane costante, cioà è indipendente dall'angolo Θ e Φ. Per l'orbitale 2pz la parte angolare dipende solo l'angolo Θ; questo significa che l'orbitale ha simmetria cilindrica attorno all'asse z, pertanto la rotazione in Φ produce sempre lo stesso valore (come già detto la parte angolare caratterizzerà la forma degli orbitali).

Dalle funzioni d'onda orbitale ψ_1s e ψ_2s alle distribuzioni di probabilità radiale

Le funzioni d'onda orbitale possono assumere segno positivo e negativo. Noi siamo interessati alla probabilità di rintracciare l'elettrone attorno al nucleo e questo valore risulta proporzionale a ψ². Siamo interessati anche alla funzione distribuzione di probabilità radiale che è la probabilità di rintracciare l'elettrone in un guscio sferico ad una certa distanza r dal nucleo (4πr²dr), che è pertanto proporzionale a (4πr²ψ²). Sia ψ² che (4πr²ψ²) assumono solo valori positivi. Nelle due immagini seguenti sono visualizzate le funzioni d'onda ψ per gli orbitali 1s e 2s (ψ_1s e ψ_2s); utilizzando i radio-buton si potranno sovrapporre le altre due funzioni descritte. (Per i commenti ai grafici si seguano le lezioni o ci si rivolga ai libri di testo):

	ψ(1,0,0) = ψ1s piani nodali: nessuno	4πr2ψ2 ψ2 ψ
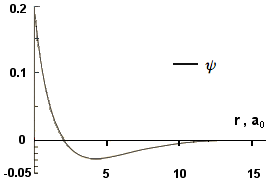	ψ(2,0,0) = ψ2s Piani nodali: uno	4πr2ψ2 ψ2 ψ

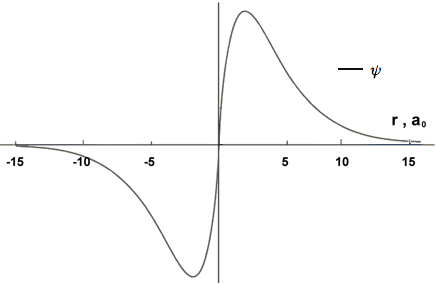
Segue il caso dell'orbitale 2pz (ψ(2,1,0)). Per esso consideriamo la distanza lungo l'asse z. Il valore dell'ampiezza della funzione d'onda risulta positivo se r ha una componente positiva nella direzione dell'asse (verso l'alto: ovvero cosΘ>0) e negativo se r che ha una componente negativa nella direzione dell'asse (verso il basso: ovvero cosΘ<0). Il grafico che segue, non in scala, è qualitativamente valido per Θ=0 (ovvero cosΘ=1). L'orbitale 2p presenta un piano nodale.

4πr2ψ2 ψ2 ψ