Lo stato gassoso (terza parte)

GAS REALI

• Le PARTICELLE non sono puntiformi ma hanno le dimensioni delle molecole che costituiscono la sostanza chimica gassosa (dimensioni dipendenti dal tipo di sostanza) 
• Le PARTICELLE sono in continuo movimento (dotate di energia cinetica) praticamente come per il gas ideale. 
• PRESENZA DI INTERAZIONI più o meno intense (dipendenti dalla natura chimica del gas) 
• Gli urti non sono perfettamente ELASTICI ED ISTANTANEI (sia con altre particelle che contro le pareti)

DEVIAZIONE DEL FATTORE DI COMPRIMIBILITA'

      L'equazione di stato dei gas ideali può essere scritta:

Per un gas ideale si può facilmente prevedere che, mettendo in grafico il precedente rapporto in funzione della pressione, si otterrà una retta parallela all'origine con intercetta di valore unitario.
Utilizzando un gas reale e procedendo a misure sperimentali dei parametri che compaiono nell'espressione, si ottengono vistose deviazione che, per ogni singolo gas dipendono dalla temperatura e pressione e, a parità di temperatura, le deviazioni risultano diverse a seconda del gas utilizzato nell'esperimento.

Nella figura seguente:
    a) fattore di comprimibilità del gas metano in funzione della temperatura;
    b) fattore di comprimibilità (T= 293 K) per alcuni gas reali

(a)	(b)

• Le deviazioni sono tanto maggiori quanto maggiore è la pressione cui viene sottoposto il gas
• La tipologia e l'entità delle deviazioni variano da gas a gas
• A pressioni sufficientemente basse (< 10 atm e poco evidenti nelle due figure (a) e (b) a causa della scala) la deviazione dal comportamento ideale è tipicamente abbastanza piccola.

Come già detto e come chiaramente illustra la figura (a), le deviazioni dal comportamento ideale dipendono dalla temperatura. In particolare, all'aumentare della temperatura le deviazioni tendono ridursi. La conclusione più ovvia e che un gas reale può, a temperatura non troppo basse e a pressioni non troppo alte, essere trattato con discreta approssimazione come un gas ideale, nel senso che l'equazione dei gas ideali può essere utilizzata per prevedere il comportamento del gas con un errore abbastanza lieve.

La più concreta ed osservabile manifestazione della non idealità di un gas reale sta nel fatto che esso può essere reso liquido abbassando la temperatura e/o aumentando la pressione.

L'equazione di Johannes Diderik van der Waals
(Leyden 1837 - Amsterdam 1923)

In ordine di tempo fu la prima equazione proposta per prevedere il comportamento dei gas reali. Si basa sul primo e terzo punto della definizione di gas reale data all'inizio di questa pagina. van der Waals, prese come riferimento l'equazione di stato dei gas ideali e propose due fondamentali correzioni: una derivante dal volume delle particelle che costituiscono il gas reale, e l'altra dovuta alle interazioni tra le molecole stesse.

Correzione del volume

      Il volume che le singole particelle "vedono" come a loro disposizione, non è il volume del recipiente che contiene il gas, ma quello "libero" che deve tenere conto del volume occupato da tutte le altre. Il volume "realmente" a disposizione del gas risulta così diminuito di una quantità b (detta covolume) che rappresenta, in prima approssimazione, il volume occupato da una mole di molecole di quello specifico gas. Il covolume risulta, pertanto, differente da gas a gas, in funzione delle specifiche dimensioni molecolari.

In breve:

Per un numero generico di moli n:

Correzione della pressione

      La pressione che il gas riesce ad esercitare sulle pareti risulta inferiore a quella idealmente aspettata perchè le particelle tendono ad attrarsi le une con le altre. Risentendo di questa attrazione verso l'interno, le particelle urtano le pareti con minor vigore (pressione minore), ovvero, come si suol dire, il gas reale tende ad autocomprimersi. La pressione che noi misureremo (Pressione reale) sarà:

In breve, ordinando:

Il termine di pressione interna dipende dal quadrato della concentrazione (attrazione reciproca) e risente anch'esso dal tipo di gas con cui si lavora (coefficiente a tipico per ogni gas reale)

Pideale = Preale + a

n 2 V 2

L'equazione di van der Waals completa:

(P + a

n 2 V 2

)  (V - n b) = n R T

L'equazione riesce a prevedere abbastanza bene il comportamento del gas reale purchè lontani dalla zona in cui esso tende a liquefare (non si può pretendere di trattare un liquido come fosse un gas). In questa equazione compaiono due termini in blu, a e b, dipendenti dal tipo di gas. Il gas reale assume così una propria identità è un comportamento specifico a seconda delle sue caratterisiche chimiche e fisiche.

L'equazione appare anche nel francobollo che gli venne dedicato. Fai click sulla miniatura di sinistra per un ingrandimento.

Nella tabella seguente vengono messi a confronto due modi diversi di scrivere l'equazione di stato dei gas ideali con la corrispondente equazione per i gas reali secondo van der Waals (sono evidenziate le correzioni):

Ideale
van der Waals

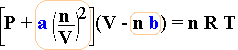
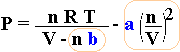
Nella tabella successiva vengono elencati i valori dei coefficienti a e b per alcune sostante gassose. Senza entrare in dettaglio facciamo notare che il gas reale che manifesta un comportamento quasi ideale è l'elio per il quale, infatti, i coefficienti a e b risultano essere molto piccoli.

Costanti di Van der Waals per alcune sostanze
Sostanza	a (L2 atm/mol2)	b (L/mol)
He (elio)	0.0341	0.0237
Ne (neon)	0.211	0.0171
Ar (argon)	1.345	0.0322
Kr (cripton)	2.318	0.0398
Xe (xenon)	4.194	0.0511
H2	0.244	0.0266
O2	1.36	0.0380
N2	1.39	0.0391
CO	1.48	0.0398
CH4	2.25	0.0428
CO2	3.59	0.0427
NH3	4.17	0.0371
H2O	5.46	0.0305
CCl4	20.4	0.1383

DIFFUSIONE ED EFFUSIONE (caso dei gas)

Il fenomeno della diffusione di un gas consiste nell'espansione-mescolamento di un gas verso un altro gas (o una miscela di gas es. aria) o espansione verso il vuoto. La diffusione (espansione) verso il vuoto è molto veloce perchè le molecole dei gas si muovono a velocità molto elevate mentre la diffusione-mescolamento contro un altro gas risulta macroscopicamente lenta.
Consideriamo due contenitori chiusi contenenti due gas diversi (rosso e verde) alla pressione di una atmosfera (1), con quello superiore capovolto. I due contenitori vengono aperti e rapidamente richiusi uno sull'altro mettendo a contatto le due aperture (2). La continua agitazione molecolare produrrà il mescolamento che non avverrà come una rapida espansione dei gas nei confronti del vuoto ma, a causa degli urti che ostacoleranno l'avanzamento dei due gas il mescolamento-diffusione avverrà in tempi piuttosto lunghi se non lo si aiuta mediante qualche tipo di agitazione (3).

Alla temperatura di 25°C il mescolamento completo di due gas (1 atm) in due contenitori alti circa 25 cm, può richiedere un tempo superiore a 30 minuti in funzione delle dimensioni molecolari e da eventuali interazioni tra i gas.
Il contenitore superiore poteva essere già aperto e contenere quindi il gas aria. Non ho usato l'aria come esempio perchè, trattandosi di una miscela, avrebbe provocato una piccola confusione grafica a causa della necessità di distinguere azoto e ossigeno; il fenomeno si sarebbe verificato in maniera pressoché analoga.
Se il contenitore del gas rosso viene aperto a contatto con l'aria, si verificherà la diffusione-mescolamento con l'aria: dell'aria entrerà nel contenitore e del gas si diffonderà verso l'esterno e, se il gas rosso presenta un particolare odore, il nostro naso lo avvertirà dopo un po' di tempo. Il diffondersi di molecole odorose nell'aria spesso avviene abbastanza rapidamente perchè al normale processo di diffusione (lento) si aggiungono rimescolamenti macroscopici dovuti alla presenza di moti convettivi e ventilazioni di varia origine.
Link su youTube - Link su Rai Education

Il fenomeno chiamato effusione consiste nell'espansione di un gas attraverso un piccolo foro verso un contenitore in cui era stato fatto il vuoto. La quantità di gas che attraversa il foro nell'unità di tempo dipende dalla velocità quadratica media che è funzione della temperatura e della massa molecolare del gas.